|
1、椭圆曲线(ECC)的算法基础: *椭圆曲线的公式: y²=X³+aX+b,其中a、b还有一些条件,这里不赘述; *椭圆曲线上的某个点的切线P的交叉点的对称点R=n*P,这个过程是由先用A、B两个点加法推导过来的,这里不赘述。 加密算法是利用已知n和P,比较容易计算出Q, 但是已知Q和P就很难计算出n(基于当今数学的发展水平)。 利用Q作为公钥,n作为私钥进行加密,其中P为双方约定的某个起点(也是下文第4点中提到的G). 所以 公钥Q=私钥n*P,理解下文需要先记住这个点。 *曲线运算法则:椭圆形曲线的加减乘法与自然数加减乘法有一样的交换律和结合律, 比如A+B+C=A+C+B, A*B*C=C*B*A. *相同安全强度下,ECC的密钥长度远小于RSA或传统DH(例如256位ECC ≈ 3072位RSA). *运算规则的推导如下:
*图1中在曲线上找到已知两个点P和Q画一条直线与曲线相交于-R,再找出-R的对称点R, 在曲线运算中数学家定义的加法就是R=P+Q(注意这是曲线加法,不是自然数的加法,而且运算量也是比较大); *图2中的C=A+B, D=A+C, E=A+D, 从而可以推导出E=A+A+C=A+A+A+B *图3中的P就是曲线的切点,这个点可以从图1中将P和Q慢慢接近后可得到,图中的r=P+P=2P; 如果r依照图2中的方法继续运算1次r=2P+P=3P 再继续1次r=3P+P=4P,一直运算下去可以得到r=nP,n表示经过多少次的‘乘运算’; 2、算法约定: *双方约定曲线名称、基点 G、素数域等; 其中基点G(generator),也就是曲线起点,这是一个不变的数值,且公开已知的 ; *假定一方叫Alice,拥有一对私钥a和公钥A,私钥不公开,只公开公钥,其中公钥A=a*G ; *假定另一方叫Bob,拥有一对私钥b和公钥B,私钥不公开,只公开公钥,其中公钥B=b*G ; *由于运算量大,通常不会直接加密明文,可能使用明文的哈希值 3、加密、解密和签名、验签的过程: 签名(signature): Alice将一个明文M(message)使用私钥乘以明文的结果作为签名S=a*M,将明文和签名一起发送给Bob。 采用椭圆曲线加密的签名简称ECDSA(Elliptic Curve Digital Signature Algorithm); 验签(verify signature): Bob使用基点G乘以签名S, 得到结果V1=G*S=G*(a*M)=G*a*M, Bob再拿收到的Alice的明文M乘公钥A, 也就是V2=M*A=M*(G*a)=M*G*a=G*a*M, 判断V1是否等于V2,Bob即可知道收到的明文M与签名S是一致,认定该明文是Alice的消息。 加密(encryption): Alice生成一个随机数r,将r乘以G得到E1=rG, 引入r是为了更强的安全性, Alice将明文M与r*B相加,得到E2=M+(r*B), Alice将E1和E2这个‘点对’发送给Bob, 解密(decryption): Bob先用私钥计算Q=b*E1=b*(rG)=b*r*G 再计算E2-Q=E2-(b*r*G)=M+(r*B)-b*r*G=M+(r*b*G)-(b*r*G)=M+(r*b*G)-(r*b*G)=M。 4、介绍BLE使用的ECDH(Elliptic Curve Diffie-Hellman): *ECDH是一种基于椭圆曲线密码学(ECC)的密钥交换协议; *BLE在secure connection paring中的密钥交换过程就是采用p-256 ECDH; *我司SDK的third_party文件夹有uecc的开源库; *BLE使用ECDH生成LTK的过程如下: 1.密钥生成: * Alice生成私钥a(随机整数),计算公钥 A=a*G * Bob生成私钥 b,计算公钥 B =b*G。。 2.交换公钥: Alice和Bob通过公开信道交换公钥 A 和 B。 3.共享密钥计算: *Alice用私钥a和Bob的公钥计算出K=a*B=a*(b*G)=ab*G *Bob用私钥b和Alice的公钥计算K=b*A=b(a*G)=ab*G。 最终双方得到相同的共享密钥K,通常取其坐标的哈希值作为对称加密密钥。 4.生成LTK: 在第3点中生成的共享密钥K就是BLE中的DHkey, 再结合双方交换的Mrand的和Srand, 利用AES-CMAC算法等运行后可得到LTK |


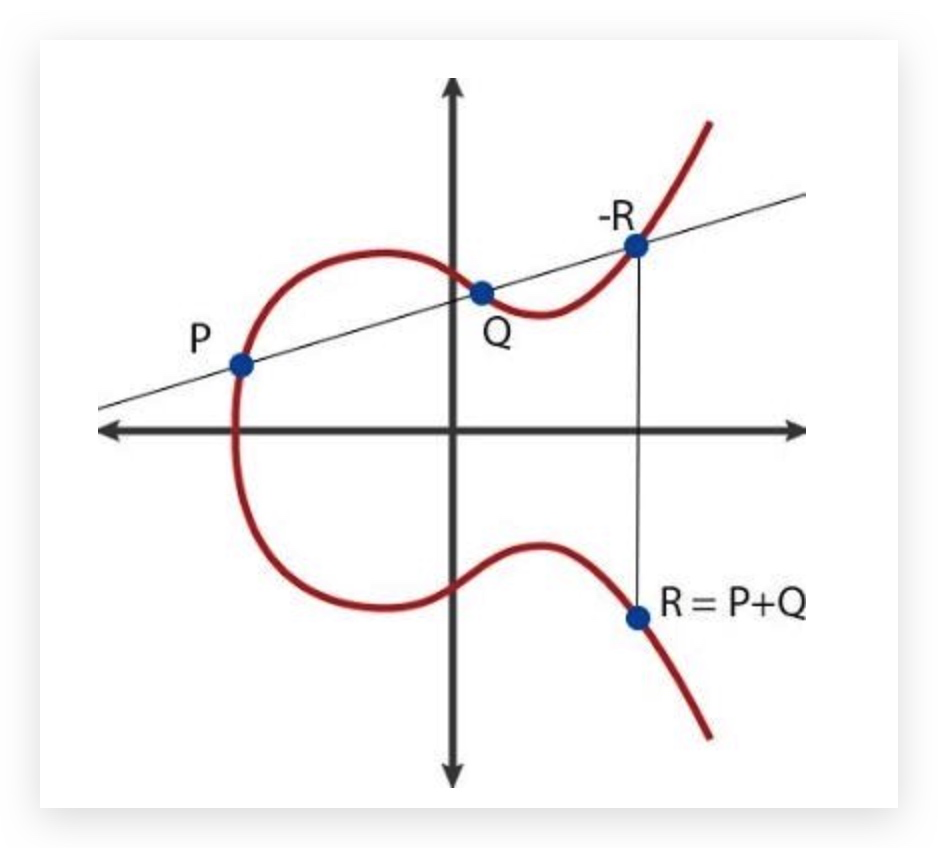 图1
图1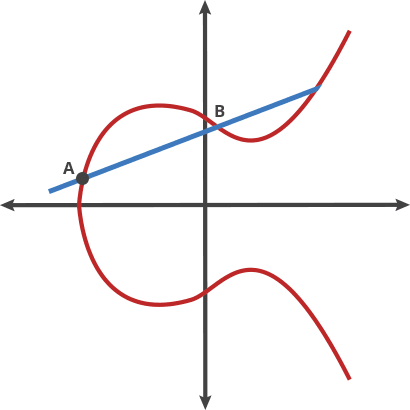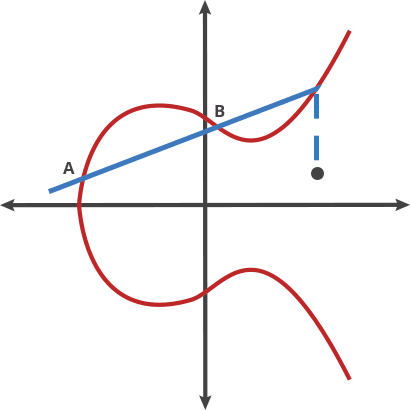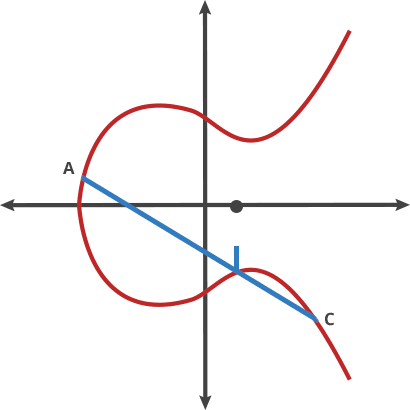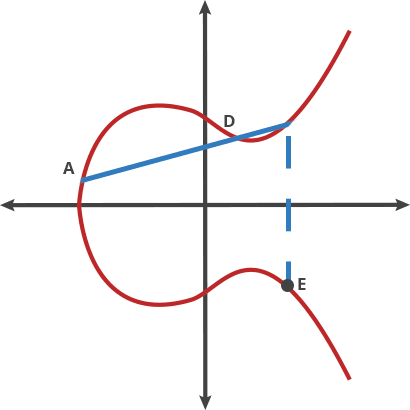 图2
图2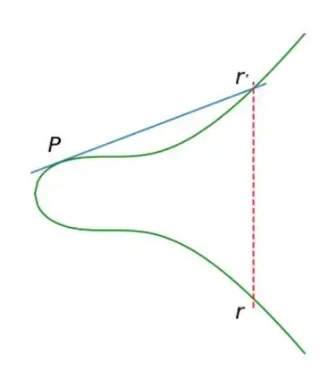 图3
图3